TensorFlow 2.0 の練習を兼ねて、混合ガウス分布 (GMM) を実装しました。
ページの末尾 に EM, Adam, RMSprop の比較アニメーションを載せています。
問題設定
ソースコード
import numpy as np
import scipy as sp
import subprocess
import tensorflow as tf
from matplotlib import pyplot as pl
# PRML の Old Faithful 間欠泉データを取得します。
# このデータはやや取得が難しく、今回は R にビルトインされているデータを使います。
def get_faithful_data():
text = subprocess.check_output(['r', '-q', '-e', 'faithful'])
text = text.decode('ascii')
text = text.splitlines()
ret = []
for line in text:
values = line.split()
if (len(values) == 3):
x = float(values[1])
y = float(values[2])
ret.append([x, y])
return np.array(ret, dtype = np.float64)
faithful = get_faithful_data()
# 二次元の散布図とガウス分布をレンタリングするためのコードです。
# ガウス分布の等高線を陰関数として描画します。
# mu は平均ベクトル、dev は x, y 軸それぞれの標準偏差です。
def draw_ring(mu, dev):
angles = np.linspace(0, 2 * np.pi, 100)
x = mu[0] + dev[0] * np.cos(angles)
y = mu[1] + dev[1] * np.sin(angles)
pl.plot(x, y, 'b-')
def draw(mu, prec):
pl.clf()
pl.plot(faithful[:, 0], faithful[:, 1], 'b+')
pl.plot(mu[:, 0], mu[:, 1], 'go')
for i in range(len(mu)):
draw_ring(mu[i], np.sqrt(1. / prec[i]))
pl.xlim(1, 6)
pl.ylim(40, 100)
pl.pause(.1)
# 比較用の EM (Expectation-Maximization) アルゴリズムの実装です。
# pi は混合率、mu は平均ベクトル、prec は分布の精度(分散の逆数)です。
# z は負担率に対応しています。
#
# 今回は簡単のため、精度行列を対角行列に制限して推定を行います。
def calc_estep(pi, mu, prec):
lpi = np.log(pi)
lprec = np.log(prec)
# アンダーフローを避けるため、対数領域で計算します。
lz = lpi[None, :] + .5 * lprec.sum(1)[None, :] - .5 * (prec[None, :, :] *
(faithful[:, None, :] - mu[None, :, :]) ** 2).sum(2)
lz -= sp.special.logsumexp(lz, axis=1)[:, None]
return np.exp(lz)
def calc_mstep(z):
pi = z.sum(0) / z.sum()
mu = (z[:, :, None] * faithful[:, None, :]).sum(0) / z.sum(0)[:, None]
prec = z.sum(0)[:, None] / (z[:, :, None] * ((faithful[:, None, :] -
mu[None, :, :]) ** 2)).sum(0)
return pi, mu, prec
def process_em(z, nstep):
for i in range(nstep):
pi, mu, prec = calc_mstep(z)
z = calc_estep(pi, mu, prec)
draw(mu, prec)
# 最急降下法を使ったパラメータ推定アルゴリズムです。
def process_sgd(z, nstep, use_adam=True):
# TensorFlow の定数と変数を定義します。
# EM アルゴリズム版と同等の初期値を作るため、一様乱数を使って M-Step を一度だけ回します。
pi, mu, prec = calc_mstep(z)
lpi = tf.Variable(np.log(pi))
mu = tf.Variable(mu)
lprec = tf.Variable(np.log(prec))
faith = tf.constant(faithful)
# オプティマイザを作成します。ここでは Adam と RMSprop の特徴が見やすくなるように
# 学習率を調整しました。
if use_adam:
opt = tf.keras.optimizers.Adam(learning_rate=.1)
else:
opt = tf.keras.optimizers.RMSprop(learning_rate=.03)
history = []
for i in range(nstep):
# GMM と観測データの KL ダイバージェンスを計算します。
# オプティマイザで自由に更新すると混合率 (pi) の総和が 1 にならないため、
# コストの計算時に pi_normal として正規化します。
#
# pi のスケールが大きく変動して予想外の動作になることを避けるため、
# ラグランジュ緩和を参考にして pi の総和が 1 に近くなるようペナルティを与えます。
def kl_loss():
penalty = tf.abs((tf.reduce_sum(tf.exp(lpi)) - 1))
lpi_normal = lpi - tf.reduce_logsumexp(lpi)
likelihood = (lpi_normal + .5 * tf.reduce_sum(lprec, axis=1))[None, :]
likelihood -= .5 * tf.reduce_sum(tf.exp(lprec)[None, :, :] *
((faith[:, None, :] - mu[None, :, :]) ** 2), axis=2)
return penalty - tf.reduce_sum(tf.reduce_logsumexp(likelihood, axis=1))
# var_list に更新したい変数 (tf.Variable) を指定し、パラメータを更新します。
opt.minimize(kl_loss, var_list=[lpi, mu, lprec])
# 現在の loss の値を計算します。
history.append(kl_loss().numpy())
# イテレーション毎にグラフを表示します。
draw(mu.numpy(), tf.exp(lprec).numpy())
# 負担率を一様乱数で初期化し、初期値とします。
# この設定では学習に多くのイテレーションが必要となり、学習アルゴリズムの特徴を調べやすくなります。
nsample = len(faithful)
nclass = 3
nstep = 10000
z = np.random.dirichlet(np.ones(nclass), nsample)
# EM, Adam, RMSprop それぞれで推論を実行します。
use_em = False
use_adam = True
if use_em:
process_em(z, nstep)
else:
process_sgd(z, nstep, use_adam)
実行結果
スクリプトの実行結果です。 動作環境は macOS Mojave (10.14) + TensorFlow 2.0.0rc0 です。
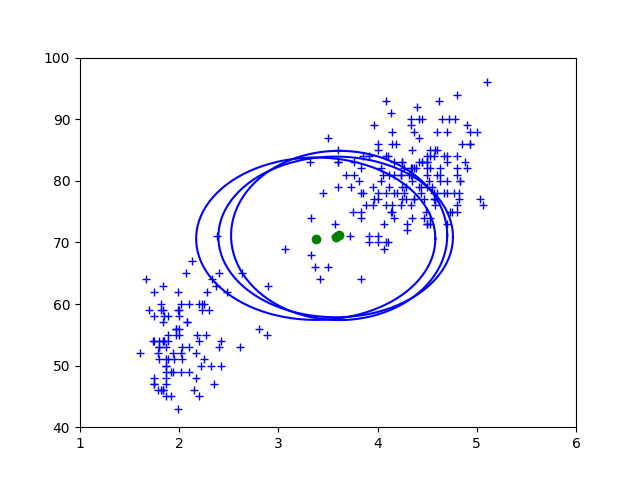
EM アルゴリズム
閉形式の更新式を使っているため、イテレーション毎に必ず尤度が上がります。
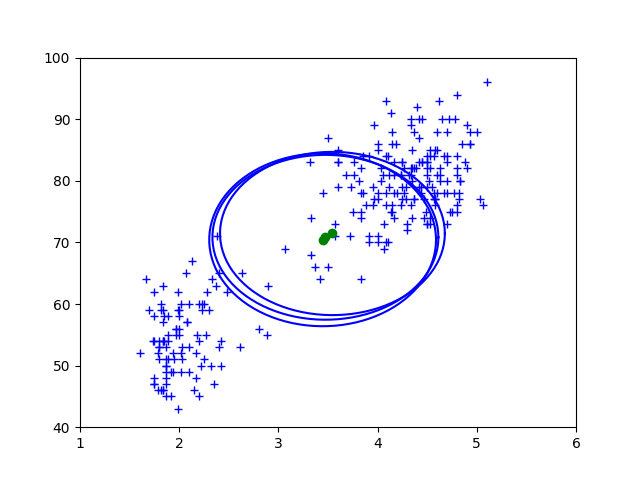
Adam
モーメンタムと各種の調整項によってパラメータを滑らかに更新します。 ハイパーパラメータの設定によっては、ゆらゆらと揺れるような動きになります。
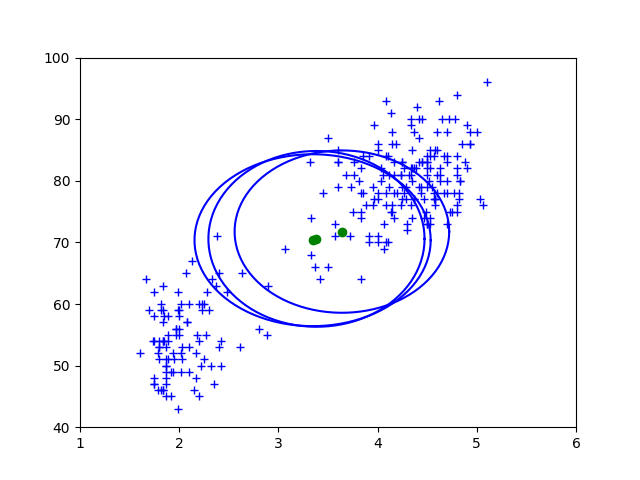
RMSprop
モーメンタム項がなく、更新によってパラメータが振動しています。
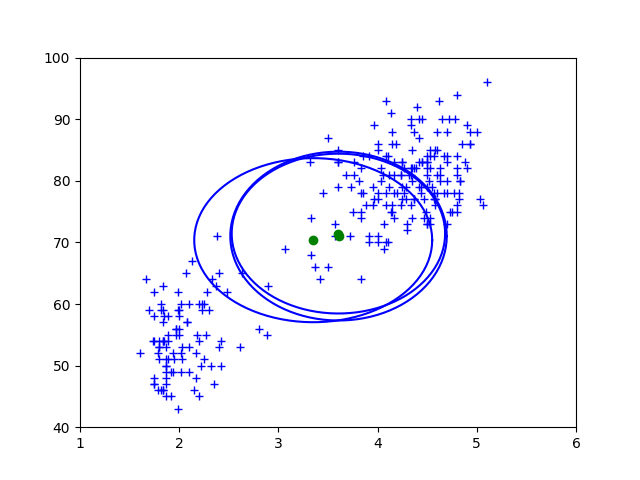
追記:Centered RMSprop
Centered RMSprop を使うと収束が改善します。
opt = tf.keras.optimizers.RMSprop(learning_rate=.03, centered=True)
RMSprop, Centered RMSprop とも中央のコンポーネントが左右どちらに振れるかは試行によってまちまちなのですが、 左のコンポーネントが収束する速さはほぼこのアニメーション通りになります。
参考文献
-
TensorFlow
https://www.tensorflow.org/ -
tf.keras.optimizers.Optimizer | TensorFlow Core r2.0
https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/optimizers/Optimizer -
tf.keras.optimizers.Adam | TensorFlow Core r2.0
https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/optimizers/Adam -
tf.keras.optimizers.RMSprop | TensorFlow Core r2.0
https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/optimizers/RMSprop -
EM アルゴリズム
https://yokaze.github.io/2017/10/11/ -
TensorFlow 2.0 で非負値行列因子分解 (NMF) を解く
https://yokaze.github.io/2019/08/12/ -
ワンライナーで平均と標準偏差を計算する - Qiita
https://qiita.com/haruyosh/items/93a794e51512f7efaaa3 -
ラグランジュ緩和問題 - 数理計画用語集
http://www.msi.co.jp/nuopt/glossary/term_c4995faa151e2d66d8ea36c8eaff94885d60c19f.html