Sliced Wasserstein GMM を実装してみた

最近話題の Sliced Wasserstein Distance (SWD) [Deshpande 2018, Deshpande 2019] を理解するため、 Kolouri らの Sliced Wasserstein Distance for Learning Gaussian Mixture Models (SWGMM) を実装しました。

以前の記事で Wasserstein 距離の解説を書いたので、こちらも是非ご参照ください。

GitHub に実装を載せました。

あらすじ

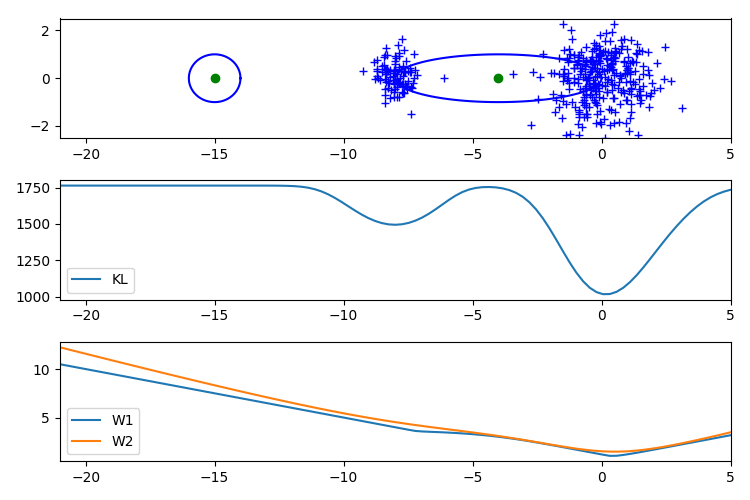
従来、観測データと生成モデルの分布を比較するために Kullback-Leibler (KL) 損失が使われてきた。しかし KL 損失を使うと勾配消失や局所解が発生するため、GAN などの高度なタスクでは上手く動かないことがある。
近年の研究から、Wasserstein 距離が勾配消失に強く、色々なタスクに応用できることが分かってきた。しかし多次元空間で Wasserstein 距離を正確に計算する方法はなく、Kantorovich-Rubinstein 双対性 [Arjovsky 2017] やエントロピー正則化 [Genevay 2018] が必要になる。
Wasserstein 距離の近似計算はそれ自体が新たなタスクになってしまうため、別の定式化を考えたい。実は Wasserstein 距離は空間が1次元の場合のみ累積密度関数のマッチングを取ることで厳密に計算できるという性質があり、これを応用したのが Sliced Wasserstein 距離 (SWD) である。
観測値が $D$ 次元ユークリッド空間 $\mathbb{R}^D$ で表現されるとき、単位球 $\mathbb{S}^{D-1}$ 上の方向ベクトル $\theta$ を使って Radon 変換を行うと1次元の Wasserstein 距離が計算できる。 Radon 変換は方向ベクトル $\theta$ の直交補空間を積分消去する操作で、ガウス分布や離散データ集合の Radon 変換は $\theta$ との内積として求まる。
Sliced Wasserstein 距離は Radon 変換された1次元空間上の Wasserstein 距離を全方向ベクトル $\mathbb{S}^{D-1}$ について積分した値である。この値は解析的に計算できないが、方向ベクトルをランダムにサンプリングすることで近似できる。この計算には学習やハイパーパラメータが存在しないため安定である。
1次元空間における離散分布と混合ガウス分布の間の Wasserstein 距離はパラメータ $\pi, \mu, \Sigma$ に対して数値的に微分可能である。このため上の手順で近似した Sliced Wasserstein 距離も微分可能となり、パラメータに対する勾配が計算できる。このアルゴリズムが Kolouri らの論文のテーマである。

図: 二つのガウス分布を使って観測データをモデル化し、左側のガウス分布の位置だけを移動した際の KL, Wasserstein-1, Wasserstein-2 損失の比較。KL 損失を使うと勾配消失が発生する上、左側の局所解に捕まって動けなくなってしまう。 Wasserstein 距離は適切な勾配を持ち、また問題の大域最適解を発見できている。 2次元の Wasserstein 距離は計算できないため、X 軸方向の損失のみ計算している。（ソースコード）

問題設定

経験分布と密度関数

観測されたデータ $X = [ x_1 \cdots x_N ]$ があり、これを多次元の混合ガウス分布 (GMM) でモデル化したい。 $\delta_x$ を Dirac 測度とすると、観測データの経験分布は

$$ \begin{align*} P_\mathrm{r} = \frac{1}{N} \sum_{n=1}^N \delta_{x_n} \end{align*} $$

と書ける。 $P_\mathrm{r}$ はルベーグ測度であり、$\mathbb{R}^D$ の部分集合 $A$ に対して $P_\mathrm{r}(A) = M/N$ （$M$ は $A$ に含まれる観測値の数）となる。また、混合ガウス分布の密度関数は

$$ \begin{align*} P_\mathrm{g} = \sum_{k=1}^K \pi_k \mathcal{N}(\mu_k, \Sigma_k) \end{align*} $$

のように書ける。$P_\mathrm{g}$ は絶対連続な測度であり、$\mathbb{R}^D$ 上の関数として扱うことができる。

$$ \begin{align*} P_\mathrm{g}(x) &= \sum_{k=1}^K \pi_k \mathcal{N}(x | \mu_k, \Sigma_k) \\ P_\mathrm{g}(A) &= \int_A \sum_{k=1}^K \pi_k \mathcal{N}(x | \mu_k, \Sigma_k) dx \end{align*} $$

Radon 変換

$\theta$ を方向ベクトル、$\theta^\perp$ を $\theta$ の直交補空間とする。 $t$ を $\theta$ 軸上の座標とすると、確率測度 $P$ の Radon 変換は次のように書ける。

$$ \begin{align*} \mathcal{R}P(t, \theta) &= \int_{\theta^\perp} P(t\theta + x) dx & (x \in \theta^\perp)\\ \mathcal{R}P(T, \theta) &= P(T\theta + \theta^\perp) & (T \subset \mathbb{R}) \end{align*} $$

この積分では $\theta$ 方向に沿った座標軸だけを残し、$D-1$ 次元の直交補空間 $\theta^\perp$ を積分消去している。たとえば、次の積分は X 軸方向への Radon 変換とみなせる。

$$ \begin{align*} P(x) = \iint P(x, y, z) dy dz \end{align*} $$

離散分布と混合ガウス分布の Radon 変換

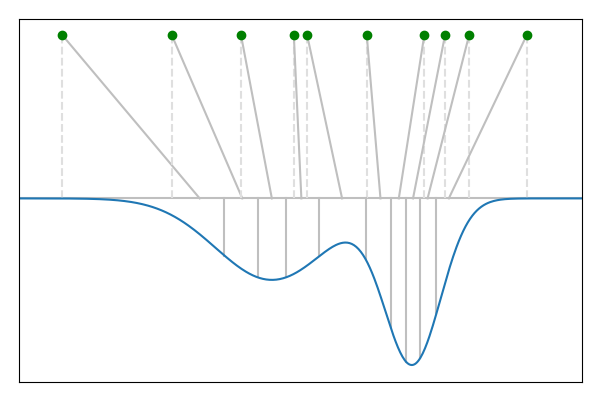
$P_\mathrm{r}$ と $P_\mathrm{g}$ の $\theta$ 軸への Radon 変換は次のように書ける。$\langle \rangle$ は内積をあらわす。

$$ \begin{align*} \mathcal{R}P_\mathrm{r} &= \frac{1}{N} \sum_{n=1}^N \delta_{\langle \theta, x_n \rangle} \\ \mathcal{R}P_\mathrm{g} &= \sum_{k=1}^K \pi_k \mathcal{N}(\langle \theta, \mu \rangle, \theta^\mathrm{T}\Sigma\theta) \end{align*} $$

1次元 Wasserstein 距離の性質

確率測度 $P$ と $Q$ の Wasserstein 距離を計算する方法は主に 2 つあり、最適な輸送方法を考えて Wasserstein 距離の積分を計算する方法と、Kantorovich-Rubinstein 双対性を使って双対問題を解く方法がある。 1次元の輸送問題では最適輸送を式で表現することができ、$P$ の点 $x_p$ における質量は $\tilde{Q}^{-1}(\tilde{P}(x_p))$ に輸送される。ここで $\tilde{P}, \tilde{Q}$ は $P, Q$ の累積密度関数である。これは、左の質量は左に、右の質量は右に、$P$ から $Q$ へ順序を保って輸送されるということを意味している。

今回のように $P$ が離散分布、$Q$ が連続分布の場合もこの応用として考えられる。 $P$ の確率が $x_1 \cdots x_N$ に $1/N$ ずつあるとすると、$x_n$ へ輸送されるのは $Q$ の密度のうち

$$ \begin{align*} \frac{n - 1}{N} < \int_{-\infty}^x Q(x) dx < \frac{n}{N} \end{align*} $$

を満たす範囲である。この範囲は $Q$ の累積密度関数の逆関数を使って

$$ \begin{align*} \tilde{Q}^{-1}\left(\frac{n - 1}{N}\right) < x < \tilde{Q}^{-1}\left(\frac{n}{N}\right) \end{align*} $$

とあらわすことができる。したがって、$P$ と $Q$ の Wasserstein 距離は

$$ \begin{align*} W_p(P, Q) = \left\{ \sum_{n=1}^N \int_{\tilde{Q}^{-1}((n-1)/N)}^{\tilde{Q}^{-1}(n/N)} |x - x_n|^p Q(x) dx \right\}^{1/p} \end{align*} $$

と書ける。特に、$Q$ が1次元ガウス分布、$p = 1, 2$ の場合は次の公式を使って積分できる。

$$ \begin{align*} \int_a^b e^{-x^2} dx &= \frac{\sqrt{\pi}}{2}\{ \mathrm{erf}(b) - \mathrm{erf}(a) \} \\ \int_a^b x e^{-x^2} dx &= - \frac{1}{2}(e^{-b^2} - e^{-a^2}) \\ \int_a^b x^2 e^{-x^2} dx &= \frac{\sqrt{\pi}}{4}\{\mathrm{erf}(b) - \mathrm{erf}(a) \} - \frac{1}{2}(b e^{-b^2} - a e^{-a^2}) \end{align*} $$

$Q$ が混合ガウス分布の場合はさらに対応が必要である。 GMM の累積密度関数の逆関数は簡単に計算できないため、累積密度関数が狭義単調増加であることを利用してバイナリサーチを使うと $\tilde{Q}^{-1}(x)$ が計算できる。また、累積密度関数の逆関数の微分が累積密度関数の微分の逆数であることを利用すると、自動微分に対応できる。

注意

実際の推論で必要になるのは $W_p$ の積分値ではなく $W_p$ を各パラメータで微分した値なので、実はこの値を苦労して求める必要はありません。実際、元論文では $W_p$ を表現することなく微分形だけを書き下しています。また、積分形を計算してしまうことにより $p$ が整数の場合にしか対応できなくなるという問題も起こります（著者実装は全ての正の実数 $p$ に対応しています）。

図: 離散分布と連続分布のアライメント。

Sliced Wasserstein 距離

$W_p(P, Q)$ を確率測度 $P$ と $Q$ の $p$-Wasserstein 距離とする。このとき、$P$ と $Q$ の Sliced Wasserstein 距離を次の通り定義する。

$$ \begin{align*} SW_p(P, Q) = \left\{ \int_{\mathbb{S}^{D-1}} W_p(\mathcal{R}P(\cdot, \theta), \mathcal{R}Q(\cdot, \theta)) d\theta \right\}^\frac{1}{p} \end{align*} $$

このとき $SW_p$ は距離の定義を満たす。この値は直接計算することができないが、有限個の方向ベクトルをランダムにサンプリングすることで近似できる。

$$ \begin{align*} SW_p(P, Q) \simeq \frac{1}{L} \sum_{l=1}^L W_p(\mathcal{R}P(\cdot, \theta_l), \mathcal{R}Q(\cdot, \theta_l)) \end{align*} $$

以上の定式化を使うと、$SW_p$ の近似値を計算グラフで表現することができる。したがって、この値を損失関数として各パラメータの勾配を計算することができる。

ソースコード

ここでは簡単のため、共分散行列の対角成分のみを推定しています。混合率と精度の対数 $\ln \pi_k, \ln \Lambda_k$ を変数とすることで、これらの変数が負の値にならないことを保証しています。

import numpy as np
import scipy as sp
import subprocess
import tensorflow as tf
from matplotlib import pyplot as pl

# PRML の Old Faithful 間欠泉データを取得します。
# このデータはやや取得が難しく、今回は R にビルトインされているデータを使います。
def get_faithful_data():
    text = subprocess.check_output(['r', '-q', '-e', 'faithful'])
    text = text.decode('ascii')
    text = text.splitlines()
    ret = []
    for line in text:
        values = line.split()
        if (len(values) == 3):
            x = float(values[1])
            y = float(values[2])
            ret.append([x, y])
    return np.array(ret, dtype=np.float64)

# オプティマイザの動作を改善するため、観測データを正規化します。
faithful = get_faithful_data()
faithful -= np.mean(faithful, axis=0)[None, :]
faithful /= np.std(faithful, axis=0)[None, :]

# 二次元の散布図とガウス分布をレンタリングするためのコードです。
# ガウス分布の等高線を陰関数として描画します。
# mu は平均ベクトル、dev は x, y 軸それぞれの標準偏差です。
def draw_ring(mu, dev, alpha=1):
    angles = np.linspace(0, 2 * np.pi, 100)
    x = mu[0] + dev[0] * np.cos(angles)
    y = mu[1] + dev[1] * np.sin(angles)
    pl.plot(x, y, 'b-', alpha=alpha)

def draw_directions(directions):
    for i in range(len(directions)):
        d = directions[i]
        pl.plot([d[0] * -5, d[0] * 5], [d[1] * -5, d[1] * 5], 'b-', alpha=.125)

def draw(pi, mu, var, directions):
    draw_directions(directions)
    pl.plot(faithful[:, 0], faithful[:, 1], 'b+', alpha=.5)
    pl.plot(mu[:, 0], mu[:, 1], 'go')
    for i in range(len(mu)):
        draw_ring(mu[i], np.sqrt(var[i]))
        draw_ring(mu[i], np.sqrt(pi[i] / pi.mean()) * np.sqrt(var[i]), alpha=.25)
    pl.xlim(-2.5, 2.5)
    pl.ylim(-2.5, 2.5)

# ガウス積分を計算します。
def integrate_emx2(a, b):
    return .5 * np.sqrt(np.pi) * (tf.math.erf(b) - tf.math.erf(a))

def integrate_xemx2(a, b):
    return .5 * (tf.exp(-a * a) - tf.exp(-b * b))

def integrate_x2emx2(a, b):
    A = .25 * np.sqrt(np.pi) * tf.math.erf(a) - .5 * a * tf.exp(-a * a)
    B = .25 * np.sqrt(np.pi) * tf.math.erf(b) - .5 * b * tf.exp(-b * b)
    return B - A

# EM アルゴリズムの M ステップを実行します。
# 今回は SWGMM の初期値を作るために使います。
# https://yokaze.github.io/2019/08/30/
def calc_mstep(z):
    pi = z.sum(0) / z.sum()
    mu = (z[:, :, None] * faithful[:, None, :]).sum(0) / z.sum(0)[:, None]
    var = (z[:, :, None] * ((faithful[:, None, :] - mu[None, :, :]) ** 2)).sum(0)
    var /= z.sum(0)[:, None]
    return pi, mu, var

# 負担率を一様乱数で初期化し、潜在変数の初期値を作ります。
# この設定では学習に多くのイテレーションが必要となり、学習アルゴリズムの特徴を調べやすくなります。
def sample_init_parameter():
    z = np.random.dirichlet(np.ones(nclass), len(faithful))
    pi, mu, var = calc_mstep(z)
    lpi = tf.Variable(np.log(pi))
    mu = tf.Variable(mu)
    lv = tf.Variable(np.log(var))
    return lpi, mu, lv

# Radon 変換で使う方向ベクトルを作成します。
def sample_direction():
    angle = 2 * np.pi * np.random.rand()
    return tf.constant([np.cos(angle), np.sin(angle)])

# Sliced Wasserstein 距離を近似するための方向ベクトル集合を作成します。
# fixed パラメータが指定されている場合、戻り値の一部を固定します。
def sample_directions(ndirection, fixed=None):
    if (fixed is not None):
        assert len(fixed) <= ndirection
        ret = list(fixed)
    else:
        ret = []

    while (len(ret) < ndirection):
        ret.append(sample_direction())
    ret = np.array(ret)
    return tf.constant(ret, dtype=tf.float64)

# 入力ベクトルと方向ベクトルの内積を計算し、ベクトルを射影した座標を計算します。
def project_vector(x, direction):
    if (x.shape.rank == 1):
        x = x[None, :]
    ret = tf.reduce_sum(x * direction[None, :], axis=1)
    return tf.squeeze(ret)

# 対角分散行列 diag(V) を指定した方向に射影した時の分散を計算します。
def project_variance(var, direction):
    if (var.shape.rank == 1):
        var = var[None, :]
    ret = tf.reduce_sum(var * (direction * direction)[None, :], axis=1)
    return tf.squeeze(ret)

# 1 次元ガウス分布の密度関数です。
def gaussian_pdf(x, mu, var):
    x = tf.convert_to_tensor(x, dtype=tf.float64)
    mu = tf.convert_to_tensor(mu, dtype=tf.float64)
    prec = 1. / tf.convert_to_tensor(var, dtype=tf.float64)
    if (x.shape.rank == 0):
        x = x[None]
    if (mu.shape.rank == 0):
        mu = mu[None]
        prec = prec[None]
    ret = tf.sqrt(.5 * prec[None, :] / np.pi)
    ret *= tf.exp(-.5 * prec[None, :] * (x[:, None] - mu[None, :]) *
                  (x[:, None] - mu[None, :]))
    return tf.squeeze(ret)

# 1 次元ガウス分布の累積密度関数です。
def gaussian_cdf(x, mu, var):
    x = tf.convert_to_tensor(x, dtype=tf.float64)
    mu = tf.convert_to_tensor(mu, dtype=tf.float64)
    var = tf.convert_to_tensor(var, dtype=tf.float64)
    if (x.shape.rank == 0):
        x = x[None]
    if (mu.shape.rank == 0):
        mu = mu[None]
    ret = .5 * (1 + tf.math.erf((x[:, None] - mu[None, :]) / tf.sqrt(2 * var)))
    return tf.squeeze(ret)

# 1 次元混合ガウス分布の密度関数です。
def gaussian_mixture_pdf(x, pi, mu, var):
    pi = tf.convert_to_tensor(pi, dtype=tf.float64)
    return tf.reduce_sum(pi[None, :] * gaussian_pdf(x, mu, var), axis=1)

# 1 次元混合ガウス分布の累積密度関数です。
def gaussian_mixture_cdf(x, pi, mu, var):
    pi = tf.convert_to_tensor(pi, dtype=tf.float64)
    return tf.reduce_sum(pi[None, :] * gaussian_cdf(x, mu, var), axis=1)

# 1 次元混合ガウス分布の累積密度関数の逆関数を計算します。
# この値は解析的に求まらないため、関数が単調増加であることを利用してバイナリサーチを実行します。
# この操作により計算グラフが分断されるため、tf.custom_gradient を実装して自動微分に対応します。
@tf.custom_gradient
def gaussian_mixture_cdfinv(r, pi, mu, var):
    r = tf.convert_to_tensor(r, dtype=tf.float64)
    pi = tf.convert_to_tensor(pi, dtype=tf.float64)
    mu = tf.convert_to_tensor(mu, dtype=tf.float64)
    var = tf.convert_to_tensor(var, dtype=tf.float64)
    if (r.shape.rank == 0):
        r = r[None]
    xmin = -1
    xmax = 1
    while (tf.reduce_sum(pi * gaussian_cdf(xmin, mu, var)) > r[0]):
        xmin *= 2
    while (tf.reduce_sum(pi * gaussian_cdf(xmax, mu, var)) < r[-1]):
        xmax *= 2
    xmin = tf.tile(tf.convert_to_tensor([xmin], dtype=tf.float64), r.shape)
    xmax = tf.tile(tf.convert_to_tensor([xmax], dtype=tf.float64), r.shape)
    for i in range(50):
        xmid = (xmin + xmax) * .5
        cur_ratio = tf.reduce_sum(pi[None, :] * gaussian_cdf(xmid, mu, var), axis=1)
        mask = tf.cast(r < cur_ratio, tf.float64)
        xmin = xmin * mask + xmid * (1 - mask)
        xmax = xmid * mask + xmax * (1 - mask)
    ret = (xmin + xmax) * .5

    def grad(_dx):
        gpdf = gaussian_pdf(ret, mu, var)
        gmpdf = gaussian_mixture_pdf(ret, pi, mu, var)
        _dr = _dx / gaussian_mixture_pdf(ret, pi, mu, var)
        _dpi = -tf.reduce_sum(_dx[:, None] * gaussian_cdf(ret, mu, var) /
                              gmpdf[:, None], axis=0)
        _dmu = tf.reduce_sum(_dx[:, None] * pi[None, :] * gpdf /
                             gmpdf[:, None], axis=0)
        _dvar = tf.reduce_sum(_dx[:, None] * pi[None, :] / (2 * var[None, :]) *
                              (ret[:, None] - mu[None, :]) * gpdf /
                              gmpdf[:, None], axis=0)
        return [_dr, _dpi, _dmu, _dvar]
    return ret, grad

# 観測データ X と 1 次元混合ガウス分布の Wasserstein 距離を計算します。
# 1-Wasserstein と 2-Wasserstein のみ実装しています。
def gaussian_mixture_wasserstein_loss(x, pi, mu, var, order):
    # 混合ガウス分布とのアライメントを計算するため、入力データをソートします。
    x = tf.sort(x)
    nx = x.shape[0]

    # 分布の精度を計算します。
    prec = 1. / var

    # 混合ガウス分布からの輸送コストを計算するため、分布を入力データと同じ数に分割します。
    # 1-Wasserstein の積分は絶対値の存在により輸送方向（左右）で符号が変わるため、
    # 右向き輸送と左向き輸送の切り替え位置をあわせて計算します。
    ratio = tf.cast(tf.linspace(1. / nx, 1 - 1. / nx, nx - 1), tf.float64)
    partition = gaussian_mixture_cdfinv(ratio, pi, mu, var)
    partition_left = tf.concat([[-1e+10], partition], axis=0)
    partition_right = tf.concat([partition, [1e+10]], axis=0)
    partition_mid = tf.minimum(tf.maximum(partition_left, x), partition_right)

    # 積分のため変数変換を行います。
    integral_left = (partition_left[:, None] - mu[None, :]) * \
        tf.sqrt(.5 * prec)[None, :]
    integral_mid = (partition_mid[:, None] - mu[None, :]) * \
        tf.sqrt(.5 * prec)[None, :]
    integral_right = (partition_right[:, None] - mu[None, :]) * \
        tf.sqrt(.5 * prec)[None, :]

    if (order == 1):
        loss_left = (x[:, None] - mu[None, :]) * \
            integrate_emx2(integral_left, integral_mid)
        loss_left -= 1. / tf.sqrt(.5 * prec[None, :]) * \
            integrate_xemx2(integral_left, integral_mid)
        loss_left *= tf.cast(1. / tf.sqrt(np.pi), tf.float64)
        loss_right = 1. / tf.sqrt(.5 * prec[None, :]) * \
            integrate_xemx2(integral_mid, integral_right)
        loss_right -= (x[:, None] - mu[None, :]) * \
            integrate_emx2(integral_mid, integral_right)
        loss_right *= tf.cast(1. / tf.sqrt(np.pi), tf.float64)
        return pi[None, :] * (loss_left + loss_right)
    elif (order == 2):
        diff = x[:, None] - mu[None, :]
        loss = (diff * diff) * integrate_emx2(integral_left, integral_right)
        loss -= 2 * diff / tf.sqrt(.5 * prec[None, :]) * \
            integrate_xemx2(integral_left, integral_right)
        loss += 1. / (.5 * prec[None, :]) * \
            integrate_x2emx2(integral_left, integral_right)
        loss *= tf.cast(1. / tf.sqrt(np.pi), tf.float64)
        return pi[None, :] * loss
    else:
        assert False

def estimate(nstep, ndirection, fixed_directions=None, order=2, use_adam=True):
    faith = tf.constant(faithful)
    lpi, mu, lv = sample_init_parameter()

    if use_adam:
        opt = tf.keras.optimizers.Adam(learning_rate=.2)
    else:
        opt = tf.keras.optimizers.RMSprop(learning_rate=.05, centered=True)

    loss_history = []
    for istep in range(nstep):
        directions = sample_directions(ndirection, fixed_directions)

        def sw_loss():
            total_loss = 0
            for idirection in range(ndirection):
                direction = directions[idirection]
                faith_proj = project_vector(faith, direction)
                lpi_normal = lpi - tf.reduce_logsumexp(lpi)
                pi = tf.exp(lpi_normal)
                mu_proj = project_vector(mu, direction)
                var_proj = project_variance(tf.exp(lv), direction)
                projected_loss = gaussian_mixture_wasserstein_loss(faith_proj, pi, mu_proj, var_proj, order)
                total_loss += tf.reduce_sum(projected_loss)
            return total_loss / ndirection

        # 推論の過程をグラフにレンタリングします。
        # 左上から順に推論状況、X軸方向の Wasserstein 距離、累積密度関数のアライメント、
        # 右側が Sliced Wasserstein 距離の近似値です。
        def draw_figure():
            pl.clf()

            pl.subplot(321)
            lpi_normal = lpi - tf.reduce_logsumexp(lpi)
            pi = tf.exp(lpi_normal)
            draw(pi.numpy(), mu.numpy(), np.exp(lv.numpy()), directions.numpy())

            pl.subplot(323)
            direction = tf.convert_to_tensor([1, 0], dtype=tf.float64)
            faith_proj = tf.sort(project_vector(faith, direction))
            mu_proj = project_vector(mu, direction)
            var_proj = project_variance(tf.exp(lv), direction)
            loss = gaussian_mixture_wasserstein_loss(faith_proj, pi, mu_proj, var_proj, order=1)
            loss = tf.reduce_sum(loss, axis=1)
            pl.plot(faith_proj, loss, 'b+', alpha=.5)
            pl.xlim(-2.5, 2.5)
            pl.ylim(0, 0.01)

            pl.subplot(325)
            nx = faith_proj.shape[0]
            ratio = tf.cast(tf.linspace(1. / (2 * nx), (2 * nx - 1) / (2 * nx), nx), tf.float64)
            p = gaussian_mixture_cdfinv(ratio, pi, mu_proj, var_proj)
            pl.plot(faith_proj, ratio)
            pl.plot(p, ratio)
            pl.xlim(-2.5, 2.5)
            pl.ylim(0, 1)

            pl.subplot(122)
            pl.plot(loss_history)
            pl.xlim(0, nstep)
            pl.ylim(0, (loss_history[0] * 1.2).numpy())
            pl.tight_layout()

        # var_list に更新したい変数 (tf.Variable) を指定し、パラメータを更新します。
        opt.minimize(sw_loss, var_list=[lpi, mu, lv])

        # 現在の loss の値を計算します。
        loss_history.append(sw_loss() ** (1. / order))

        # イテレーション毎にグラフを表示します。
        # tight_layout が上手く動作しないため、初回のみ 2 回レンタリングを実行します。
        # （実装環境は macOS Mojave + Python3）
        draw_figure()
        if (istep == 0):
            draw_figure()
        pl.pause(.1)

# グラフの大きさを設定します。
pl.figure(figsize=[7.5, 5])

# ガウス分布の数、推論の繰り返し回数を設定します。
nclass = 5
nstep = 100

# Sliced Wasserstein 距離の近似計算に使う積分方向の数を設定します。
# 数値積分を使うため、ndirection = inf の場合厳密な計算になります。
ndirection = 5

# Sliced Wasserstein 距離の計算に固定の積分方向を加える場合はここで入力します。
fixed_directions = None
# fixed_directions = [[1, 0]]
# fixed_directions = [[1, 0], [0, 1]]
# fixed_directions = [[1., 0.], [0., 1.], [np.sqrt(2), np.sqrt(2)]]
# fixed_directions = [[1., 0.], [0., 1.], [np.sqrt(2), np.sqrt(2)], [np.sqrt(2), -np.sqrt(2)]]

# Wasserstein 距離の次数を設定します。この実装では 1 と 2 のみ対応しています。
order = 2

# Adam と RMSprop どちらを使うかを選択し、推論を行います。
use_adam = True
estimate(nstep, ndirection, fixed_directions, order, use_adam)

# 推論が終わったらグラフを表示して停止します。
pl.show()

実行結果

このプログラムを実行すると次の動作になります。

本当は Sliced Wasserstein 距離の計算に使う方向ベクトルもレンタリングされるのですが、チカチカしすぎるので消しました…。著者実装と同じく 1 イテレーションにつき 5 つの方向ベクトルを使っています。

各イテレーション毎に異なる方向ベクトルに沿った勾配が得られるため、各コンポーネントがゆらゆらと揺れています。

左中央のグラフは X 軸に沿った各データ点ごとの輸送コスト、左下は累積密度関数のアライメントです。この値はグラフを作成するために推論プロセス外で別途計算しています。

右側のグラフは推論で使用した SW 距離の近似値の履歴を表示しています。

Sliced Wasserstein 距離の性質

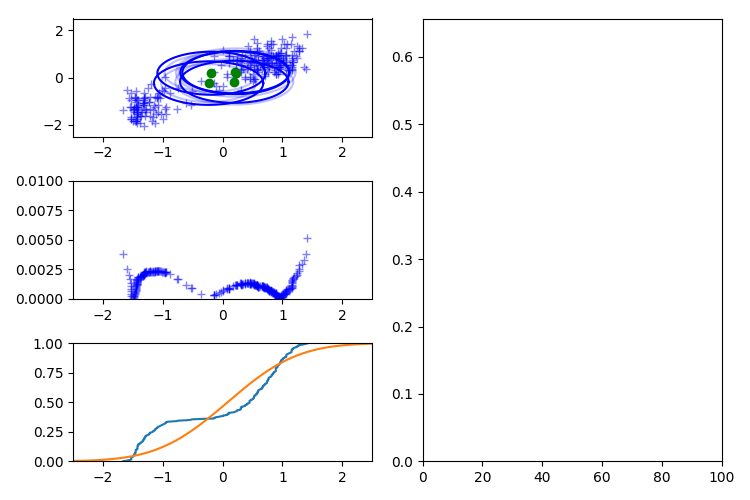
Sliced Wasserstein 距離はサンプリングされた方向に沿ってパラメータの勾配を与えるため、 X 軸のみを与え続けると Y 軸方向の学習が進みません。

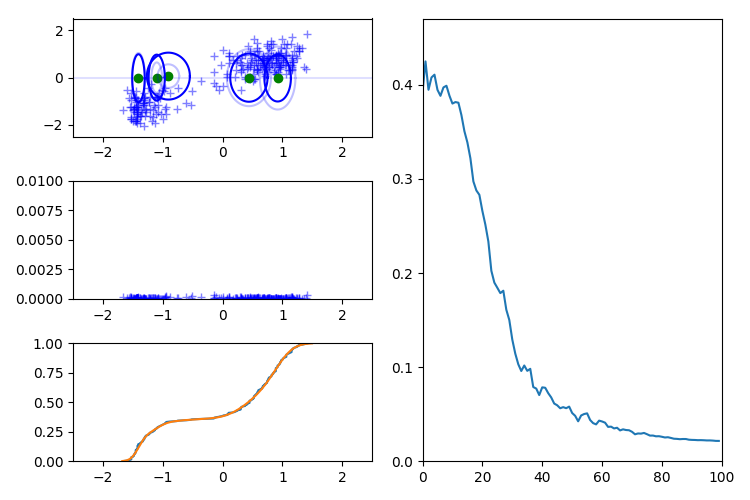
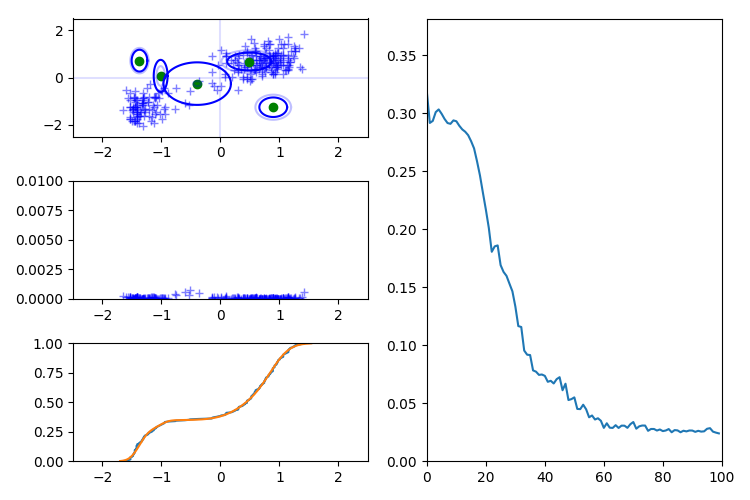
また、観測データの次元数と同じ数の方向ベクトルを与えても上手くいかないことがあります。次の例では X 軸方向、Y 軸方向に射影した密度は推定できていますが、X 軸、Y 軸をあわせた同時分布の推論に失敗しています。このため、推論の過程では観測データの次元数より多くの方向ベクトルを使う必要があります。 W2 では上手く検証できなかったので、この図のみ W1 距離で作成しています。

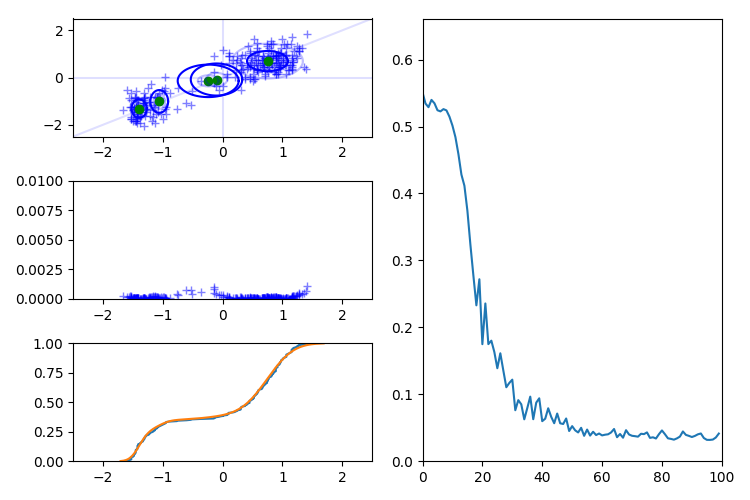
X 軸、Y 軸に加え斜めの軸を追加すると推論はほぼ正しく進みます。

参考文献

Gabriel Peyré and Marco Cuturi, “Computational Optimal Transport”, Foundations and Trends in Machine Learning, vol. 11, no. 5–6, pp. 355–607, 2019.
https://arxiv.org/abs/1803.00567
Aude Genevay, Gabriel Peyré, Marco Cuturi, “Learning Generative Models with Sinkhorn Divergences”, in Proc. AISTATS, 2018, pp. 1608–1617.
http://proceedings.mlr.press/v84/genevay18a.html
Martin Arjovsky, Soumith Chintala, and Léon Bottou, “Wasserstein Generative Adversarial Networks”, in Proc. ICML, 2017, pp. 214–223.
http://proceedings.mlr.press/v70/arjovsky17a.html
Soheil Kolouri, Gustavo K. Rohde, Heiko Hoffmann, “Sliced Wasserstein Distance for Learning Gaussian Mixture Models”, in Proc. CVPR, 2018, pp. 3427–3436.
https://arxiv.org/abs/1711.05376
Sliced Wasserstein Distance for Learning Gaussian Mixture Models （著者実装）
https://github.com/skolouri/swgmm
Sliced Wasserstein Distance for Learning Gaussian Mixture Models | 2018/07/07 CV勉強会@関東CVPR論文読み会（後編）
https://www.slideshare.net/FujimotoKeisuke/sliced-wasserstein-distance-for-learning-gaussian-mixture-models
Ishan Deshpande, Ziyu Zhang, Alexander Schwing, “Generative Modeling using the Sliced Wasserstein Distance”, in Proc. CVPR, 2018, pp. 3483–3491.
https://arxiv.org/abs/1803.11188
Ishan Deshpande, Yuan-Ting Hu, Ruoyu Sun, Ayis Pyrros, Nasir Siddiqui, Sanmi Koyejo, Zhizhen Zhao, David Forsyth, Alexander Schwing, “Max-Sliced Wasserstein Distance and its use for GANs”, in Proc. CVPR, 2019, pp. 10648–10656.
https://arxiv.org/abs/1904.05877
Max-Sliced Wasserstein Distance and its use for GANs (SlideShare)
https://www.slideshare.net/HidekiTsunashima/maxsliced-wasserstein-distance-and-its-use-for-gans